高斯牛顿法实现曲线拟合

python 高斯牛顿法曲线拟合

学习篇

发布日期: 2024-04-22

更新日期: 2024-11-03

文章字数: 1.2k

阅读时长: 6 分

本文使用高斯牛顿法实现曲线拟合

目的

一方面出于学习的目的完成这个小项目，另一方面出于为其他的同学提供一个相关的代码学习资料

拟合方程

$y=e^{ax^3+bx^2+cx+d}+w$

数据产生（随机数产生，误差服从高斯分布）

$w~\left( 0,\sigma ^2 \right)$

误差定义

$er_{i}=y_i-e^{ax_{i}^{3}+bx_{i}^{2}+cx_i+d}$

求偏导（最关键）

$\left\{ \begin{array}{l} \frac{\partial er_i}{\partial a}=-x_{i}^{3}e^{ax_{i}^{3}+bx_{i}^{2}+cx_i+d}\\ \frac{\partial er_i}{\partial a}=-x_{i}^{2}e^{ax_{i}^{3}+bx_{i}^{2}+cx_i+d}\\ \frac{\partial er_i}{\partial c}=-x_ie^{ax_{i}^{3}+bx_{i}^{2}+cx_i+d}\\ \frac{\partial er_i}{\partial d}=-e^{ax_{i}^{3}+bx_{i}^{2}+cx_i+d}\\ \end{array} \right.$

# 产生固定间隔的数组
import numpy as np

start = 0   # 起始值
stop = 1.5   # 结束值（不包含在数组中）
step = 0.01    # 间隔

arr = np.arange(start, stop, step)
# print(arr)


mean = 0    # 均值
std = 10    # 标准差
size = int((stop-start)/step)  # 数组大小

noise = np.random.normal(mean, std, size)
# print(noise)


# 生成观测数据x,y

# 定义函数参数
a = 0.5
b = 1
c = 2.0
d = -1
x=arr
obs_y=np.exp(a*x**3 + b*x**2 + c*x + d)+noise

import matplotlib.pyplot as plt
import matplotlib
matplotlib.rc("font",family='MicroSoft YaHei',weight="bold")
# 绘制图像

# 定义函数
def f(x,A):
    return np.exp(A[0]*x**3 + A[1]*x**2 + A[2]*x + A[3])

# 计算对应的 y 值
y = f(x,[a,b,c,d])

plt.plot(x, y)
plt.scatter(x, obs_y, color='red', s=10,label='Scatter Points')
plt.xlabel('x')
plt.ylabel('y')
plt.title('正确地函数图像')
plt.grid(True)
plt.show()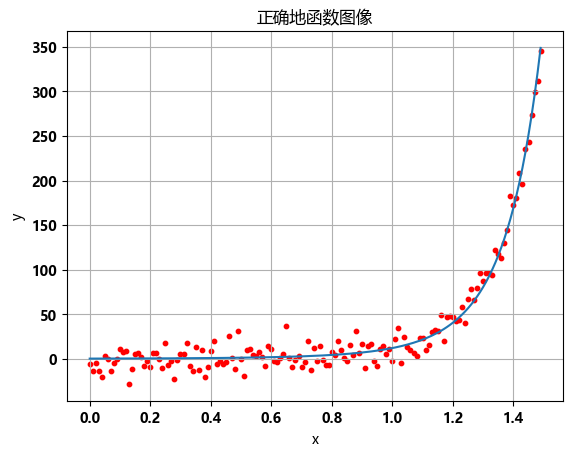

png

高斯牛顿迭代进行曲线拟合（我理解为间接平差升级版）

直接求得解析解

$V=Bx-L$ $x=\left( B^TB \right) *\left( B^TL \right)$ $\left[ \begin{array}{c} er_1\\ er_2\\ \vdots\\ er_{n-1}\\ er_n\\ \end{array} \right] =\boldsymbol{B}\left[ \begin{array}{c} \varDelta a\\ \varDelta b\\ \varDelta c\\ \varDelta d\\ \end{array} \right] -\boldsymbol{L}$ $\boldsymbol{B}=\left[ \begin{matrix} -x_{1}^{3}e^{a_0x_{1}^{3}+b_0x_{1}^{2}+c_0x_1+d_0}& \cdots& \cdots& -e^{a_0x_{1}^{3}+b_0x_{1}^{2}+c_0x_1+d_0}\\ -x_{2}^{3}e^{a_0x_{2}^{3}+b_0x_{2}^{2}+c_0x_2+d_0}& \vdots& \vdots& -e^{a_0x_{2}^{3}+b_0x_{2}^{2}+c_0x_2+d_0}\\ \vdots& \vdots& \vdots& \vdots\\ -x_{n-1}^{3}e^{a_0x_{n-1}^{3}+b_0x_{n-1}^{2}+c_0x_{n-1}+d_0}& \vdots& \vdots& -e^{a_0x_{n-1}^{3}+b_0x_{n-1}^{2}+c_0x_{n-1}+d_0}\\ -x_{n}^{3}e^{a_0x_{n}^{3}+b_0x_{n}^{2}+c_0x_n+d_0}& \cdots& \cdots& -e^{a_0x_{n}^{3}+b_0x_{n}^{2}+c_0x_n+d_0}\\ \end{matrix} \right]$ $L=\left[ \begin{array}{l} e^{a_0x_{1}^{3}+b_0x_{1}^{2}+c_0x_1+d_0}-y_1\\ e^{a_0x_{2}^{3}+b_0x_{2}^{2}+c_0x_2+d_0}-y_2\\ \vdots\\ e^{a_0x_{n-1}^{3}+b_0x_{n-1}^{2}+c_0x_{n-1}+d_0}-y_{n-1}\\ e^{a_0x_{n}^{3}+b_0x_{n}^{2}+c_0x_n+d_0}-y_{n}\\ \end{array} \right]$

# 定义a,b,c,d的初始值(随便定)
a0=0.3
b0=0.7
c0=1.6
d0=-0.7

# 定义函数,A为参数数组
def f0(x,A):
    return np.exp(A[0]*x**3 + A[1]*x**2 + A[2]*x + A[3])

# 计算对应的 y 值
y0 = f0(x,[a0,b0,c0,d0])

plt.plot(x, y)
plt.plot(x, y0)
plt.scatter(x, obs_y, color='red', s=10,label='Scatter Points')
plt.xlabel('x')
plt.ylabel('y')
plt.title('正确地函数图像')
plt.grid(True)
plt.show()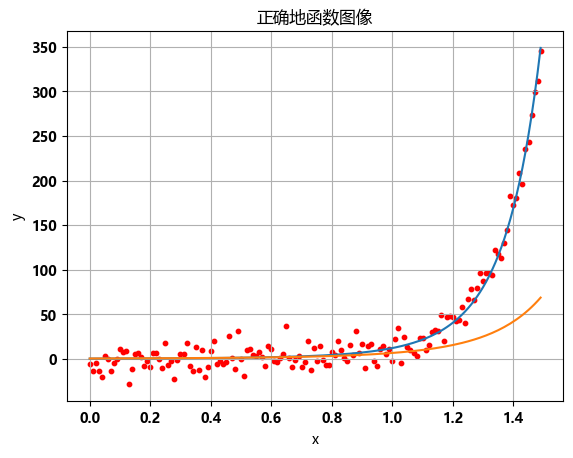

png

# 进行间接平差求解
# 构建B矩阵
a0_temp=a0
b0_temp=b0
c0_temp=c0
d0_temp=d0

approx=np.array([a0_temp,b0_temp,c0_temp,d0_temp])

# 迭代次数
n=10
dieDaiResult = np.zeros((n, 4))
# 用一个

for j in range(n):
        B=np.zeros((size,4))
        L=np.zeros((size,1))
        for i in range(size):
            B[i,0]=-x[i]**3*f0(x[i],approx)
            B[i,1]=-x[i]**2*f0(x[i],approx)
            B[i,2]=-x[i]*f0(x[i],approx)
            B[i,3]=-f0(x[i],approx)
            L[i,0]=f0(x[i],approx)-obs_y[i]

        arr_B=np.array(B)
        arr_L=np.array(L)
        tem1=np.linalg.inv(np.dot(np.transpose(arr_B),arr_B))
        tem2=np.dot(np.transpose(arr_B),arr_L)

        delta_x=np.dot(tem1,tem2)
        # 这里进行下一次迭代
        approx=approx+delta_x.flatten()
        # list_approx=approx.
        dieDaiResult[j,:]=approx

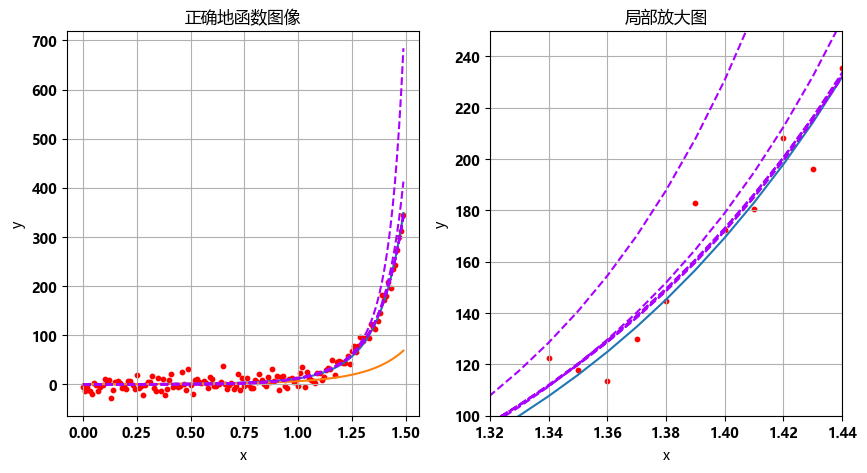
fig = plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
# 标准曲线
plt.plot(x, y)
# 初始曲线
plt.plot(x, y0)
# 迭代曲线
for i in range(n-8,n):
      xishu=dieDaiResult[i]
      print(xishu)
      tem_y=f0(x,xishu)
      plt.plot(x, tem_y,color='#aa00ff',linestyle='--')
# plt.plot(x, y1,color='#aa00ff')
plt.scatter(x, obs_y, color='red', s=10,label='Scatter Points')
# plt.plot(x, y1)
plt.xlabel('x')
plt.ylabel('y')
plt.title('正确地函数图像')
plt.grid(True)

# 创建第二个子图
plt.subplot(1, 2, 2)
# 标准曲线
plt.plot(x, y)
# 初始曲线
plt.plot(x, y0)
# 迭代曲线
for i in range(n-8,n):
      xishu=dieDaiResult[i]
      print(xishu)
      tem_y=f0(x,xishu)
      plt.plot(x, tem_y,color='#aa00ff',linestyle='--')
# plt.plot(x, y1,color='#aa00ff')
plt.scatter(x, obs_y, color='red', s=10,label='Scatter Points')
# plt.plot(x, y1)
plt.xlabel('x')
plt.ylabel('y')
plt.title('局部放大图')

# 设置局部放大范围
plt.xlim(1.32, 1.44)  # 设置 x 轴范围
plt.ylim(100, 250)   # 设置 y 轴范围
plt.grid(True)
plt.show()

[ 15.18948191 -48.88914189  58.18225421 -21.87081973]
[ 11.06123187 -37.62392869  48.70588659 -19.61002625]
[ 2.98965953 -9.4558721  16.33702568 -7.39086396]
[-0.25717518  2.86430852  0.85419677 -0.95130386]
[ 2.28260343 -6.65929933 12.58667395 -5.68529249]
[-0.53772553  3.94032672 -0.50831067 -0.38253999]
[ 2.22309202 -6.36924235 12.12862682 -5.44958593]
[-0.55472966  4.00668407 -0.59381963 -0.34621364]
[ 15.18948191 -48.88914189  58.18225421 -21.87081973]
[ 11.06123187 -37.62392869  48.70588659 -19.61002625]
[ 2.98965953 -9.4558721  16.33702568 -7.39086396]
[-0.25717518  2.86430852  0.85419677 -0.95130386]
[ 2.28260343 -6.65929933 12.58667395 -5.68529249]
[-0.53772553  3.94032672 -0.50831067 -0.38253999]
[ 2.22309202 -6.36924235 12.12862682 -5.44958593]
[-0.55472966  4.00668407 -0.59381963 -0.34621364]

png